Welcome to Faiss Documentation

Faiss

Faiss is a library for efficient similarity search and clustering of dense vectors. It contains algorithms that search in sets of vectors of any size, up to ones that possibly do not fit in RAM. It also contains supporting code for evaluation and parameter tuning.

Faiss is written in C++ with complete wrappers for Python. Some of the most useful algorithms are implemented on the GPU. It is developed primarily at FAIR, the fundamental AI research team of Meta.

What is similarity search?

Given a set of vectors \(x_i\) in dimension \(d\), Faiss builds a data structure in RAM from it. After the structure is constructed, when given a new vector \(x\) in dimension \(d\) it performs efficiently the operation:

\[j = argmin_i \lVert x - x_i \rVert\]

where \(\lVert\cdot\rVert\) is the Euclidean distance (\(L^2\)).

In Faiss terms, the data structure is an index, an object that has an add method to add \(x_i\) vectors. Note that the \(x_i\)’s are assumed to be fixed.

Computing the argmin is the search operation on the index.

This is all what Faiss is about. It can also:

• return not just the nearest neighbor, but also the 2nd nearest, 3rd, …, k-th nearest neighbor

• search several vectors at a time rather than one (batch processing). For many index types, this is faster than searching one vector after another

• trade precision for speed, ie. give an incorrect result 10% of the time with a method that’s 10x faster or uses 10x less memory

• perform maximum inner product search \(argmax_i \langle x, x_i \rangle\) instead of minimum Euclidean search. There is also limited support for other distances (L1, Linf, etc.).

• return all elements that are within a given radius of the query point (range search)

• store the index on disk rather than in RAM.

• index binary vectors rather than floating-point vectors

• ignore a subset of index vectors according to a predicate on the vector ids.

Install

The recommended way to install Faiss is through Conda:

$ conda install -c pytorch faiss-cpu

The faiss-gpu package provides CUDA-enabled indices:

$ conda install -c pytorch faiss-gpu

Note that either package should be installed, but not both, as the latter is a superset of the former.

Research foundations of Faiss

Faiss is based on years of research. Most notably it implements:

• The inverted file from “Video google: A text retrieval approach to object matching in videos.”, Sivic & Zisserman, ICCV 2003. This is the key to non-exhaustive search in large datasets. Otherwise all searches would need to scan all elements in the index, which is prohibitive even if the operation to apply for each element is fast

• The product quantization (PQ) method from “Product quantization for nearest neighbor search”, Jégou & al., PAMI 2011. This can be seen as a lossy compression technique for high-dimensional vectors, that allows relatively accurate reconstructions and distance computations in the compressed domain.

• The three-level quantization (IVFADC-R aka IndexIVFPQR) method from “Searching in one billion vectors: re-rank with source coding”, Tavenard & al., ICASSP’11.

• The inverted multi-index from “The inverted multi-index”, Babenko & Lempitsky, CVPR 2012. This method greatly improves the speed of inverted indexing for fast/less accurate operating points.

• The optimized PQ from “Optimized product quantization”, He & al, CVPR 2013. This method can be seen as a linear transformation of the vector space to make it more amenable for indexing with a product quantizer.

• The pre-filtering of product quantizer distances from “Polysemous codes”, Douze & al., ECCV 2016. This technique performs a binary filtering stage before computing PQ distances.

• The GPU implementation and fast k-selection is described in “Billion-scale similarity search with GPUs”, Johnson & al, ArXiv 1702.08734, 2017

• The HNSW indexing method from “Efficient and robust approximate nearest neighbor search using Hierarchical Navigable Small World graphs”, Malkov & al., ArXiv 1603.09320, 2016

• The in-register vector comparisons from “Quicker ADC : Unlocking the Hidden Potential of Product Quantization with SIMD”, André et al, PAMI’19, also used in [“Accelerating Large-Scale Inference with Anisotropic Vector Quantization” <https://arxiv.org/abs/1908.10396>`_, Guo, Sun et al, ICML’20.

• The binary multi-index hashing method from “Fast Search in Hamming Space with Multi-Index Hashing”, Norouzi et al, CVPR’12.

• The graph-based indexing method NSG from “Fast Approximate Nearest Neighbor Search With The Navigating Spreading-out Graph” <https://arxiv.org/abs/1707.00143>`_, Cong Fu et al, VLDB 2019.

• The Local search quantization method from “Revisiting additive quantization”, Julieta Martinez, et al. ECCV 2016 and “LSQ++: Lower running time and higher recall in multi-codebook quantization”, Julieta Martinez, et al. ECCV 2018.

• The residual quantizer implementation from “Improved Residual Vector Quantization for High-dimensional Approximate Nearest Neighbor Search”, Shicong Liu et al, AAAI’15.

A general paper about product quantization and related methods: “A Survey of Product Quantization”, Yusuke Matsui, Yusuke Uchida, Hervé Jégou, Shin’ichi Satoh, ITE transactions on MTA, 2018.

The overview image below is from that paper (click on the image to enlarge it):

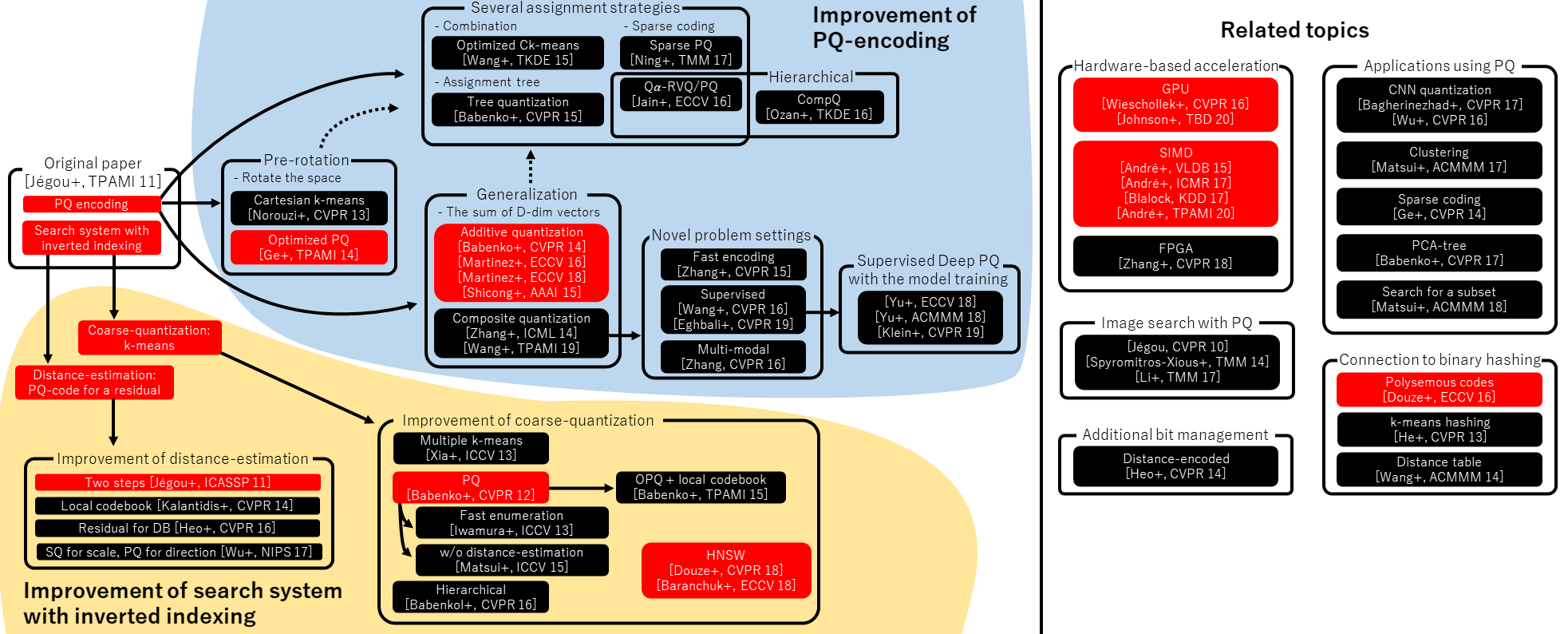
Image credit: Yusuke Matsui, thanks for allowing us to use it!

Methods that are implemented in Faiss are highlighted in red.

Key to all references

André+, “Cache Locality is not Enough: High-performance Nearest Neighbor Search with Product Quantization Fast Scan”, VLDB 15
André+, “Accelerated Nearest Neighbor Search with Quick ADC”, ICMR 17
André+, “Quicker ADC : Unlocking the Hidden Potential of Product Quantization with SIMD”, IEEE TPAMI 20
Babenko and Lempitsky, “The Inverted Multi-index”, CVPR 12
Babenko and Lempitsky, “Additive Quantization for Extreme Vector Compression”, CVPR 14
Babenko and Lempitsky, “The Inverted Multi-index”, IEEE TPAMI 15
Babenko and Lempitsky, “Tree Quantization for Large-scale Similarity Search and Classification”, CVPR 15
Babenko and Lempitsky, “Efficient Indexing of Billion-scale Datasets of Deep Descriptors”, CVPR 16
Babenko and Lempitsky, “Product Split Trees”, CVPR 17
Bagherinezhad+, “LCNN: Lookup-based Convolutional Neural Network”, CVPR 17
Baranchuk+, “Revisiting the Inverted Indices for Billion-Scale Approximate Nearest Neighbors”, ECCV 18
Blalock and Guttag, “Bolt: Accelerated Data Mining with Fast Vector Compression”, KDD 17
Eghbali and Tahvildari, “Deep Spherical Quantization for Image Search”, CVPR 19
Douze+, “Polysemous Codes”, ECCV 16
Douze+, “Link and code: Fast Indexing with Graphs and Compact Regression Codes”, CVPR 18
Ge+, “Optimized Product Quantization”, IEEE TPAMI 14
Ge+, “Product Sparse Coding”, CVPR 14
He+, “K-means Hashing: An Affinity-preserving Quantization Method for Learning Binary Compact Codes”, CVPR 13
Heo+, “Short-list Selection with Residual-aware Distance Estimator for K-nearest Neighbor Search”, CVPR 16
Heo+, “Distance Encoded Product Quantization”, CVPR 14
Iwamura+, “What is the Most Efficient Way to Select Nearest Neighbor Candidates for Fast Approximate Nearest Neighbor Search?”, ICCV 13
Jain+, “Approximate Search with Quantized Sparse Representations”, ECCV 16
Jégou+, “Product Quantization for Nearest Neighbor Search”, IEEE TPAMI 11
Jégou+, “Aggregating Local Descriptors into a Compact Image Representation”, CVPR 10
Jégou+, “Searching in One Billion Vectors: Re-rank with Source Coding”, ICASSP 11
Johnson+, “Billion-scale Similarity Search with GPUs”, IEEE TBD 20
Klein and Wolf, “End-to-end Supervised Product Quantization for Image Search and Retrieval”, CVPR 19
Kalantidis and Avrithis, “Locally Optimized Product Quantization for Approximate Nearest Neighbor Search”, CVPR 14
Li+, “Online Variable Coding Length Product Quantization for Fast Nearest Neighbor Search in Mobile Retrieval”, IEEE TMM 17
Martinez+, “Revisiting Additive Quantization”, ECCV 16
Martinez+, “LSQ++: Lower Running Time and Higher Recall in Multi-codebook Quantization”, ECCV 18
Matsui+, “PQTable: Fast Exact Asymmetric Distance Neighbor Search for Product Quantization using Hash Tables”, ICCV 15
Matsui+, “PQk-means: Billion-scale Clustering for Product-quantized Codes”, ACMMM 17
Matsui+, “Reconfigurable Inverted Index”, ACMMM 18
Ning+, “Scalable Image Retrieval by Sparse Product Quantization”, IEEE TMM 17
Norouzi and Fleet, “Cartesian k-means”, CVPR 13
Ozan+, “Competitive Quantization for Approximate Nearest Neighbor Search”, IEEE TKDE 16
Spyromitros-Xious+, “A Comprehensive Study over VLAD and Product Quantization in Large-scale Image Retrieval”, IEEE TMM 14
Yu+, “Product Quantization Network for Fast Image Retrieval”, ECCV 18
Yu+, “Generative Adversarial Product Quantization”, ACMMM 18
Wang+, “Optimized Distances for Binary Code Ranking”, ACMMM 14
Wang+, “Optimized Cartesian k-means”, IEEE TKDE 15
Wang+, “Supervised Quantization for Similarity Search”, CVPR 16
Wang and Zhang, “Composite Quantization”, IEEE TPAMI 19
Wieschollek+, “Efficient Large-scale Approximate Nearest Neighbor Search on the GPU”, CVPR 16
Wu+, “Multiscale Quantization for Fast Similarity Search”, NIPS 17
Wu+, “Quantized Convolutional Neural Networks for Mobile Devices”, CVPR 16
Xia+, “Joint Inverted Indexing”, ICCV 13
Zhang+, “Composite Quantization for Approximate Nearest Neighbor Search”, ICML 14
Zhang+, “Sparse Composite Quantization”, CVPR 15.
Zhang+, “Collaborative Quantization for Crossmodal Similarity Search”, CVPR 16
Zhang+, “Efficient Large-scale Approximate Nearest Neighbor Search on OpenCL FPGA”, CVPR 18

Legal

See the Terms of Use and Privacy Policy.